Fast and Efficient finetuning of LLMs: QLoRA
#12 Advanced Generative AI: Efficient Finetuning of Quantised LLMs
Introduction
Large Language Models (LLMs) have revolutionized natural language processing, demonstrating remarkable capabilities across a wide range of tasks. However, fine-tuning these massive models for specific applications presents significant challenges, particularly in terms of computational resources and memory requirements. Enter QLoRA (Quantised Low-Rank Adaptation), an innovative technique that combines the benefits of quantization and low-rank adaptation to enable cheap, fast and efficient fine-tuning of LLMs when hardware resources are limited.
In this blog post, we'll explore QLoRA's quantisation and low-rank adaptation, implementation, and impact on training LLMs.

Background - Quantisation and LoRA
Before we delve into QLoRA, let's establish a foundational understanding of its key components, i.e. Quantisation and Low-Rank adaptation (LoRA)
Quantization
Quantization is a technique for reducing the precision of a model's parameters and activations. By representing these values with fewer bits, quantization significantly reduces memory usage and computational requirements, often with minimal impact on model performance.
Precision-based Quantisation
Here are different precision quantisation representation data that are currently used for training models:
FP32 (32-bit floating-point):
Standard precision is used in most deep-learning training.
Provides a wide dynamic range (1.18 × 10^-38 to 3.4 × 10^38) and high precision. It has 32 bits, 8 exponent bits and 23 fraction bits.
The memory required to store one value is 4 bytes.
Serves as the baseline for comparing other quantization methods.
FP16 (16-bit floating-point):
Reduces memory usage by half compared to FP32.
Dynamic range of 6.10 × 10^-5 to 6.55 × 10^4. It has 16 bits, 5 exponent bits and 10 fraction bits.
The memory required to store one value is 2 bytes.
Commonly used in mixed-precision training to balance accuracy and efficiency.
BF16 (Brain Floating Point):
Uses 16 bits like FP16 but with a different distribution: 16 bits, 8 exponent bits, and 7 fraction bits.
BF16 is a compromise between FP32 and FP16. It is designed to maintain much of FP32's dynamic range while offering the memory and computational benefits of a 16-bit format.
Offers a larger dynamic range than FP16 (1.18 × 10^-38 to 3.4 × 10^38), making it more suitable for training.
The memory required to store one value is 2 bytes.
Increasingly popular in modern AI hardware due to its balance of range and precision.
INT8 (8-bit integer):
Represents values using 8 bits, typically in the range -128 to 127 or 0 to 255. It has 8 bits, 8 exponent bits and 7 fraction bits.
Dramatically reduces memory usage and increases inference speed.
Requires careful calibration to maintain accuracy, often using techniques like quantization-aware training or post-training quantization.
INT4 (4-bit integer):
Pushes the boundaries of low-precision representation, using only 4 bits per value.
Requires advanced techniques to maintain model quality.
The focus of recent research, including QLoRA, for ultra-efficient model compression.
Quantization Schemes
A quantization scheme is a method for mapping a large set of input values to a smaller set of output values. It is typically used to reduce the precision of data representation. For example, a quantization scheme will be used to convert and represent data from FP32 format to BF16 or INT8 format.
Some important quantization factors to be considered are:
Scaling Factor:
The value is used to convert between the original floating-point values and the quantised integer values.
It helps maintain the relative relationships between values while mapping them to a smaller integer range.
Formula: scale = (float_max - float_min) / (int_max - int_min)
Usage: quantized_value = round(original_value / scale)
Zero-point:
The zero-point is the integer value that represents the real-value zero in the quantized space.
It allows the representation of both positive and negative values using only unsigned integers.
Formula: zero_point = round(-float_min / scale)
Usage: quantized_value = round(original_value / scale) + zero_point
Based on the above parameters, some important quantization schemes include the following:
Linear Quantization:
Maps floating-point values to integers using a linear scaling factor and zero-point.
Quantization formula: q = round(x / scale) + zero_point
Dequantization formula: x = (q - zero_point) * scale
Simple to implement but may not capture the distribution of weights effectively.
Non-linear Quantization:
It uses non-linear mapping between floating-point and quantized values.
Can better represent the typical distribution of weights in neural networks, which often follow a normal or log-normal distribution.
Examples include logarithmic quantization and the NormalFloat scheme used in QLoRA.
Symmetric vs Asymmetric Quantization:
Symmetric: Uses a zero-point at 0, simplifying computations. Formula:
q = round(x / scale)Asymmetric: Allows for a non-zero offset, potentially capturing the weight distribution better. Uses the full formula:
q = round(x / scale) + zero_point
Now, let’s understand the Low-Rank Adaptation in detail.
Low-Rank Adaptation (LoRA) in Depth
LoRA, introduced by Hu et al. (2021), is a parameter-efficient fine-tuning (PEFT) method that freezes the pre-trained model weights and injects trainable low-rank matrices into each layer of the transformer architecture.
The fundamental idea behind LoRA is to represent the weight updates during fine-tuning as the product of two low-rank matrices rather than updating the entire model. This approach significantly reduces the number of trainable parameters while allowing for effective model adaptation to new tasks.
Mathematical Formulation of LoRA
Pre-trained LLMs have a low intrinsic dimension and can still learn effectively despite being randomly projected to a smaller space.
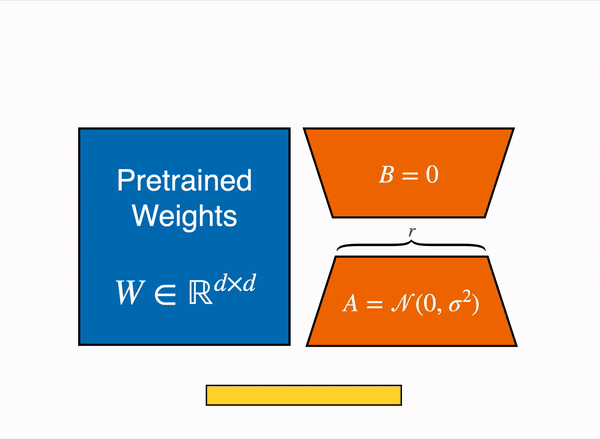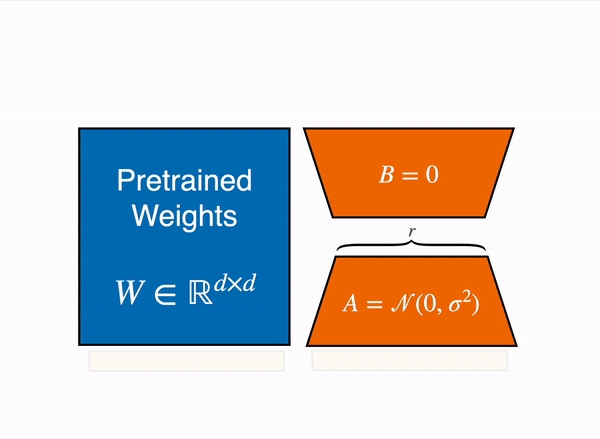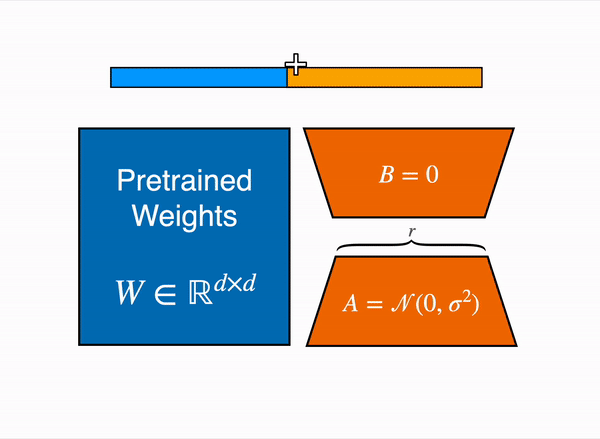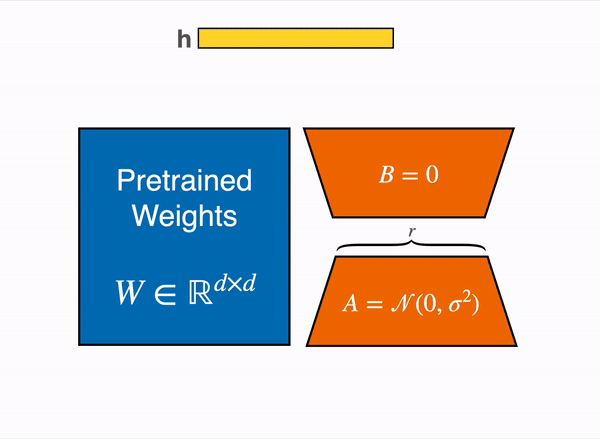
Let W₀ ∈ ℝᵈˣᵈ be the pre-trained weights of a layer in the original model. During fine-tuning with LoRA, instead of directly updating W₀, we introduce a low-rank update:
W = W₀ + BA
Where:
B ∈ ℝᵈˣʳis a matrix of dimensiond × rA ∈ ℝʳˣᵈis a matrix of dimensionr × dr is the rank of the update (typically much smaller than d and k)
The product BA represents the weight update and only A and B are trained during fine-tuning.
The above weight matrix weight decomposition is applied to the self-attention modules of the transformer. Therefore, only these modules will be trained during training while the remaining pre-trained model weights are frozen.
Key Components of LoRA
Rank (r):
Determines the expressiveness of the update.
A lower rank means fewer parameters but potentially less adaptability.
Typically, it ranges from 1 to 64, with 8 or 16 being common choices.
The number of trainable parameters introduced by LoRA is
2 * r * (d + d)for each adapted layer.
Scaling Factor (α):
Used to adjust the magnitude of the LoRA update.
The actual update is scaled:
α(BA) / rIt helps in balancing the contribution of the pre-trained weights and the LoRA update.
It can be thought of as an additional hyperparameter controlling the learning rate of LoRA parameters.
Target Modules:
Specifies which layers or sub-modules of the model to apply LoRA to.
Common choices include attention layers (query and value projections) in transformer models.
Selecting appropriate target modules can significantly impact the efficiency-performance trade-off.
LoRA in Practise
During fine-tuning, LoRA is implemented as follows:
Initialization:
LoRA matrices (A and B) are typically initialized randomly using a normal distribution with a small variance.
The scaling factor α is set to a small value (e.g., 1) at the start of training.
Training Process:
During the forward pass, the LoRA update is added to the output of the target modules (as shown in the figure above)
y = W₀x + BAxGradients are computed with respect to A and B using standard backpropagation, leaving W₀ unchanged.
The effective learning rate for LoRA parameters is scaled by
α/r.
Inference:
For efficient inference, the LoRA updates can be merged with the original weights: W = W₀ + BA
This allows for using the adapted model without additional computational overhead during inference.
Now, let’s understand the big picture of how QLoRa is implemented as a combination of LoRA and Quantization.
QLoRA: Combining Quantisation and LoRA
QLoRA, introduced by Dettmers et al. (2023), integrates advanced quantization techniques with LoRA to create a highly efficient fine-tuning method for large language models.
Before we delve into the specifics of the QLoRa workflow, we should note some key innovations introduced in the QLoRA paper.
Key Innovations
4-bit NormalFloat Quantization
Normal float is a novel quantization data type optimized for training neural networks while maintaining performance levels.
Assumes a normal distribution of weights, which is common in trained neural networks.
Uses a non-linear quantization scheme to provide better precision for values near zero.
Outperforms other 4-bit quantization methods for large language models.
The NormalFloat quantization process involves:
Estimating the parameters (μ, σ) of the normal distribution that best fits the weight tensor.
Defining non-linear quantization boundaries based on the cumulative distribution function (CDF) of the normal distribution.
Mapping weights to 4-bit integers based on these boundaries.
4-bit Normal Float is the datatype used to quantise and store base model weights during QLoRA training.
Double Quantization
Double quantization is a technique that further reduces memory usage:
First, it quantizes model weights to 4-bit precision using NormalFloat.
Then, it quantizes the resulting quantization constants (scaling factors and zero-points) to 8-bit precision.
This two-step process significantly reduces the memory footprint of quantization constants, which can be substantial in large models.
Paged Optimizers
Paged optimizers efficiently manage memory by:
Utilizing CPU memory as a backup when GPU memory is exhausted.
Implementing a sophisticated paging system to swap data between GPU and CPU memory.
Minimizing the performance impact of using CPU memory through careful optimization and prefetching strategies.
Integration of Quantization and LoRA
QLoRA combines quantization and LoRA in a synergistic manner:
Quantized Base Model:
The pre-trained model weights (W₀) are quantized to 4-bit precision using NormalFloat.
This drastically reduces the memory footprint of the base model.
Full-precision LoRA Updates:
LoRA matrices (A and B) are kept at higher precision (typically 16-bit, i.e. BF16) during training.
This allows for accurate gradient computation and weight updates.
Quantization-aware Training:
During the forward pass, quantized weights are dequantized, the LoRA update is applied, and the result is requantized.
This process ensures that the model learns to perform well within the constraints of quantization.
Memory-efficient Optimization:
Paged optimizers manage the memory of both the quantized base model and the full-precision LoRA parameters.
Gradient accumulation is used to simulate larger batch sizes without increasing memory requirements.
End-to-End QLoRA Workflow
Load the pre-trained model and quantize it to 4-bit precision using NormalFloat.
Add LoRA adapters to the quantized model, initializing them in 16-bit precision (BF16)
Use paged optimizers and gradient accumulation for memory-efficient training.
During training, perform quantization-aware forward and backward passes.
Update only the LoRA parameters, keeping the quantized base model fixed.
For inference, merge the LoRA updates with the quantized base model or keep them separate for task-specific adaptation.
This combination of techniques allows QLoRA to fine-tune models with billions of parameters on consumer-grade hardware, democratizing access to state-of-the-art language models.
Now that we have understood the theory of how QLoRA works in detail let’s implement it in code and fine-tune a large language model.
Implementation of QLoRA
First, Install the necessary libraries:
Let's walk through a practical implementation of QLoRA using the Hugging Face Transformers and PEFT libraries.
pip install transformers peft bitsandbytes accelerateLoad and Quantize the model.
Here, we are loading a 6.7 billion-parameter model in a 4-bit NormalFloat datatype with double quantization enabled. The LoRA parameters are loaded in the BF16 datatype.
import torch
from transformers import AutoModelForCausalLM, AutoTokenizer, BitsAndBytesConfig
model_name = "facebook/opt-6.7b" # Example large model
bnb_config = BitsAndBytesConfig(
load_in_4bit=True,
bnb_4bit_use_double_quant=True,
bnb_4bit_quant_type="nf4",
bnb_4bit_compute_dtype=torch.bfloat16
)
model = AutoModelForCausalLM.from_pretrained(model_name, quantization_config=bnb_config, device_map="auto")
tokenizer = AutoTokenizer.from_pretrained(model_name)Configure LoRA
Convert the pre-trained model into the LoRA model by adding the LoRA adapters and specifying parameters like rank (r), alpha, and target modules.
from peft import LoraConfig, get_peft_model
peft_config = LoraConfig(
r=8,
lora_alpha=32,
target_modules=["q_proj", "v_proj"],
lora_dropout=0.05,
bias="none",
task_type="CAUSAL_LM"
)
model = get_peft_model(model, peft_config)Load and Prepare a Dataset
For this example, let’s use the IMDb dataset from the datasets library to fine-tune our LLM.
from datasets import load_dataset
dataset = load_dataset("imdb") # Example dataset
def tokenize_function(examples):
return tokenizer(examples["text"], truncation=True, max_length=512)
tokenized_datasets = dataset.map(tokenize_function, batched=True, remove_columns=["text"])Configure Training Arguments
Let’s configure the training arguments before we start training the model using the transformers library. Note the optimizer is set as paged_adamw_8bit to efficiently manage memory with the CPU as a backup.
from transformers import TrainingArguments
training_args = TrainingArguments(
output_dir="./results",
num_train_epochs=3,
per_device_train_batch_size=4,
gradient_accumulation_steps=4,
learning_rate=2e-4,
fp16=True,
save_total_limit=3,
logging_steps=100,
optim="paged_adamw_8bit"
)Train the model
from transformers import Trainer
trainer = Trainer(
model=model,
args=training_args,
train_dataset=tokenized_datasets["train"],
eval_dataset=tokenized_datasets["test"],
tokenizer=tokenizer,
)
trainer.train()Post training the model is saved for further inference.
Conclusion
QLoRA (Quantized Low-Rank Adaptation) represents a significant leap forward in model fine-tuning. By combining quantization techniques with low-rank adaptation, QLoRA dramatically reduces the memory footprint required for training while maintaining model quality. This breakthrough allows for faster, more efficient fine-tuning of large language models on consumer-grade hardware, opening up new possibilities for customization and specialization of AI models.
The advent of QLoRA, alongside other innovative training methods like LoRA, PEFT, and instruction fine-tuning, is democratizing access to powerful language models. These techniques are making it possible for researchers, developers, and organizations of all sizes to work with and adapt state-of-the-art LLMs for specific applications. As these methods continue to evolve, we're moving closer to a future where advanced AI capabilities are not limited to tech giants but are accessible to a global community of innovators.
References
Dettmers, T., et al. (2023). QLoRA: Efficient Finetuning of Quantized LLMs. arXiv preprint arXiv:2305.14314.
Hu, E. J., et al. (2021). LoRA: Low-Rank Adaptation of Large Language Models. arXiv preprint arXiv:2106.09685.
https://huggingface.co/blog/4bit-transformers-bitsandbytes
If you enjoyed this blog, please click the ❤️ button, share it with your peers, and subscribe for more content. Your support helps spread the knowledge and grow our community. Thank you!