Implementing GPT-Style Attention: A Step-by-Step Guide with PyTorch
Learn how to build and optimize attention mechanisms for transformer models, from basic self-attention to the multi-head attention architecture used in state-of-the-art language models
Introduction
Attention mechanisms have revolutionized the field of natural language processing (NLP) in recent years, enabling models to effectively capture long-range dependencies and achieve state-of-the-art performance on a wide range of tasks. At the heart of modern language models like the Transformer and GPT series lies the self-attention mechanism, a powerful tool for relating different positions within an input sequence.
In this blog post, we'll explore the inner workings of attention, starting from the limitations of traditional approaches and building up to the efficient multi-head attention used in today's cutting-edge models. You can follow this blog post along with this Colab notebook.

Recap: The Problem with Modeling Long Sequences
Recurrent Neural Networks (RNNs) and encoder-decoder models have been widely used for processing sequential data in natural language processing tasks. However, these architectures face several challenges when dealing with long sequences:
Information Bottleneck Problem: RNNs and encoder-decoder models compress the entire input sequence into a fixed-size hidden state vector. As the sequence length grows, it becomes increasingly difficult to pack all the necessary information into this fixed-size representation. Important details from earlier parts of the sequence can be lost or overwritten as the hidden state is updated at each step, making it challenging to capture long-range dependencies.
Vanishing or Exploding Gradient Problem: During training, as the gradient signal is backpropagated through time, it can either decay exponentially (vanishing) or grow exponentially (exploding).
Vanishing gradients make it difficult for the model to learn long-range dependencies, as the gradient signal becomes too weak to effectively update earlier parts of the network.
Exploding gradients can cause the model to become unstable and diverge during training.
In encoder-decoder models, the decoder has limited access to the context from the input sequence. The fixed-size hidden state from the encoder is the only information available to the decoder at each generation step, which can be insufficient for capturing all the relevant context. This is particularly problematic for tasks like machine translation, where understanding the entire source sequence is crucial for generating accurate translations.
Furthermore, RNNs and encoder-decoder models process the input sequence sequentially, one token at a time. This sequential processing can be time-consuming, especially for long sequences, as the computation cannot be easily parallelized. Each hidden state update depends on the previous hidden state, creating an inherent sequential dependency that limits the ability to take advantage of modern hardware like GPUs that excel at parallel processing.
These limitations motivated the development of attention mechanisms, which allow the model to selectively focus on different parts of the input sequence during processing. By enabling the model to access and utilize relevant information from the entire sequence, attention mechanisms can effectively capture long-range dependencies and overcome the limitations of fixed-size hidden state representations.
Capturing Dependencies with Attention Mechanisms
To address the limitations of RNNs and encoder-decoder models, researchers introduced attention mechanisms. Attention allows the model to selectively focus on different parts of the input sequence during processing, enabling it to capture long-range dependencies more effectively.
One of the first attention mechanisms proposed was the Bahdanau attention, introduced in 2014 for neural machine translation. In this approach, the decoder can attend to relevant parts of the source sequence at each generation step, rather than relying solely on the fixed-size hidden state from the encoder. This is achieved by computing attention weights that determine the importance of each source token for the current decoding step.
The attention mechanism works by calculating a compatibility score between the current decoder hidden state and each encoder hidden state. These scores are then normalized using a softmax function to obtain attention weights. The weighted sum of the encoder hidden states, based on the attention weights, forms the context vector that provides relevant information to the decoder at each step.
By allowing the decoder to access and utilize information from the entire source sequence, the Bahdanau attention mechanism enables the model to capture long-range dependencies and generate more accurate translations. This approach laid the foundation for subsequent developments in attention mechanisms.
Building upon this idea, the Transformer architecture, introduced in the influential paper "Attention Is All You Need" by Vaswani et al. in 2017, took attention to the next level with the self-attention mechanism. Self-attention extends the attention concept to capture dependencies within a single sequence, rather than just between the encoder and decoder.
In self-attention, each token in the input sequence attends to all other tokens in the sequence, allowing the model to capture rich, context-dependent representations. This mechanism enables the model to directly learn the relationships and dependencies between different positions in the sequence, without relying on recurrent or convolutional operations.
The self-attention mechanism forms the core of the Transformer architecture and has revolutionized natural language processing. It has led to the development of powerful language models like BERT, GPT, and their variants, which have achieved state-of-the-art performance on a wide range of tasks, including language understanding, generation, and translation.
By leveraging attention mechanisms, particularly self-attention, models can effectively capture long-range dependencies, handle variable-length sequences, and process information in parallel. This has greatly enhanced the ability of models to understand and generate coherent and contextually relevant language.
In the following sections, we will dive deeper into the details of self-attention and explore its implementation in modern language models.
Simplified Self-Attention Mechanism
To gain a better understanding of how self-attention works, let's start with a simplified version of the mechanism and walk through the computation step by step. Consider an input sequence X of length 6, where each token is represented by a 3-dimensional embedding vector. The goal of self-attention is to compute a new representation for each token that incorporates information from the entire sequence. This is achieved by calculating attention weights between pairs of tokens and using these weights to compute weighted sums of the input embeddings.
First, we compute the dot product between each pair of token embeddings. The dot product serves as a measure of similarity between tokens, indicating how much they should attend to each other. In PyTorch, we can compute the dot products efficiently using matrix multiplication:
import torch
inputs = torch.tensor(
[[0.43, 0.15, 0.89], # Your (x^1)
[0.55, 0.87, 0.66], # journey (x^2)
[0.57, 0.85, 0.64], # starts (x^3)
[0.22, 0.58, 0.33], # with (x^4)
[0.77, 0.25, 0.10], # one (x^5)
[0.05, 0.80, 0.55]] # step (x^6)
)
attn_scores = inputs @ inputs.T
In the code above, attn_scores[i][j] represents the dot product between the embeddings of tokens i and j. The resulting attn_scores matrix captures the similarity scores between all pairs of tokens.
Next, we apply the softmax function to each row of the attn_scores matrix to obtain the attention weights. The softmax function normalizes the scores, converting them into probabilities that sum up to 1. This ensures that the attention weights can be interpreted as the relative importance of each token for a given token:
attn_weights = torch.softmax(attn_scores, dim=-1)After applying the softmax function, attn_weights[i][j] represents the normalized attention weight indicating how much token i attends to token j.
Finally, we compute the self-attended representations by taking a weighted sum of the input embeddings using the attention weights:
context_vecs = attn_weights @ inputsThe resulting context_vecs matrix contains the self-attended representations for each token. Each row in context_vecsis a weighted sum of the input embeddings, where the weights are determined by the attention weights. This allows each token to incorporate information from the entire sequence, weighted by the relevance of each token.
This simplified version of self-attention demonstrates the core idea of allowing tokens to attend to each other and compute new representations based on the entire sequence. However, in practice, the self-attention mechanism used in Transformer models includes additional components, such as trainable weight matrices and scaling factors, which we will explore in the next section.
Math Behind Self-Attention
In the previous section, we explored a simplified version of self-attention that directly used the input embeddings to compute attention scores and context vectors. However, in practice, the self-attention mechanism used in Transformer models incorporates trainable weight matrices to project the inputs into query, key, and value representations before computing the attention scores.
In self-attention, each input vector xi is projected onto three distinct vectors: query qi, key ki, and value vi.
These projections are performed via learnable weight matrices Wq, Wk, and Wv, resulting in:
These weight matrices are initialized randomly and optimized during training.
The simplified matrix representation, where the query, key, and value matrices are computed as a single operation, is given by:
The working of the above attention calculation is explained in the next section.
Adding Trainable Weights to Self-Attention
The query, key, and value matrices (Q, K, V) are obtained by multiplying the input embedding matrix X with learned weight matrices W_query, W_key, and W_value, respectively:
import torch.nn as nn
d_in = 3
d_out = 2
W_query = nn.Linear(d_in, d_out)
W_key = nn.Linear(d_in, d_out)
W_value = nn.Linear(d_in, d_out)
print(W_query)
# Calculate queries, keys and values
queries = W_query(inputs)
keys = W_key(inputs)
values = W_value(inputs)Here, d_in represents the input embedding dimension, and d_out represents the output dimension of the projected queries, keys, and values. The weight matrices W_query, W_key, and W_value are initialized randomly and learned during the training process.
By projecting the inputs into separate query, key, and value spaces, the model can learn to capture different aspects of the input embeddings that are relevant for computing attention. This allows for more expressive and flexible representations compared to directly using the input embeddings.
After obtaining the queries, keys, and values, the attention scores are computed as the scaled dot product between the queries and keys:
attn_scores = queries @ keys.T / keys.shape[-1]**0.5
print(attn_scores)The scaling factor (the square root of the key dimension) is introduced to mitigate the effect of large magnitudes in the dot products, which can lead to extremely small gradients when passed through the softmax function. This scaling helps stabilize the training process and improve convergence.
Once the attention scores are computed, the rest of the self-attention mechanism remains the same as in the simplified version. The attention weights are obtained by applying the softmax function to the scores, and the context vectors are computed as the weighted sum of the values using the attention weights.
To encapsulate this computation in a more compact and reusable form, we can define a Python class that implements the self-attention mechanism with trainable weights:
class SelfAttention(nn.Module):
def __init__(self, d_in, d_out):
super().__init__()
self.W_query = nn.Linear(d_in, d_out)
self.W_key = nn.Linear(d_in, d_out)
self.W_value = nn.Linear(d_in, d_out)
def forward(self, x):
queries = self.W_query(x)
keys = self.W_key(x)
values = self.W_value(x)
attn_scores = queries @ keys.T
attn_weights = torch.softmax(attn_scores / keys.shape[-1]**0.5, dim=-1)
context_vecs = attn_weights @ values
return context_vecs
The SelfAttention class uses PyTorch's nn.Linear module to define the trainable weight matrices W_query, W_key, and W_value. The forward method performs the self-attention computation, taking the input embeddings x and returning the context vectors.
By incorporating trainable weights into the self-attention mechanism, Transformer models can learn to adapt the attention computation to the specific requirements of the task at hand. This flexibility and expressiveness have contributed to the success of Transformer-based models in various natural language processing tasks.
Causal Attention: Masking Future Tokens
In certain tasks, such as language modeling or text generation, it's crucial to prevent the self-attention mechanism from accessing information from future tokens. This is where causal attention, also known as masked attention, comes into play.
Causal attention restricts the self-attention computation to only consider the tokens up to the current position in the sequence. In other words, when computing the attention scores for a given token, only the tokens that appear before it in the sequence are considered.
To achieve this, we modify the attention weight matrix by applying a mask that sets the upper triangular part of the matrix to negative infinity. This effectively prevents the model from attending to future tokens.
Here's an example of how to create the mask and apply it to the attention scores:
import torch
def create_mask(context_length):
mask = torch.triu(torch.ones(context_length, context_length), diagonal=1)
return mask.bool()
context_length = attn_scores.shape[0]
mask = create_mask(context_length)
attn_scores = attn_scores.masked_fill(mask, -torch.inf)
print(attn_scores)
In the code above, we create a mask using PyTorch's torch.triu function, which sets the elements above the main diagonal to 1 and the rest to 0. We then convert the mask to a boolean tensor and use it to fill the upper triangular part of the attn_scores matrix with negative infinity.
By setting the masked positions to negative infinity, we ensure that the softmax function will assign zero attention weights to those positions, effectively ignoring the future tokens.
After applying the mask, we proceed with the rest of the self-attention computation as usual, applying the softmax function to obtain the attention weights and computing the context vectors.
attn_weights = torch.softmax(attn_scores / keys.shape[-1]**0.5, dim=1)
print(attn_weights)It's worth noting that causal attention is particularly important in autoregressive models like GPT, where the model generates tokens sequentially and should only have access to the previously generated tokens at each step.
Adding Dropout
In addition to masking future tokens, we can also incorporate dropout regularization to the attention weights. Dropout helps prevent overfitting by randomly setting a fraction of the attention weights to zero during training. This encourages the model to rely on a broader set of tokens and reduces the risk of memorizing specific patterns.
Here's an example of how to apply dropout to the attention weights:
dropout = nn.Dropout(p=0.1)
attn_weights = dropout(attn_weights)In the code above, we create an instance of PyTorch's nn.Dropout module with a dropout probability of 0.1. We then apply the dropout to the attn_weights matrix, randomly setting 10% of the attention weights to zero and increasing the remaining values in the matrix by 10%.
By incorporating causal attention and dropout regularization, we can effectively mask future tokens and improve the generalization ability of our self-attention-based models.
To encapsulate the causal attention mechanism, we can define a CausalAttention class that inherits from the SelfAttention class and adds the masking and dropout functionality:
import torch.nn as nn
class CausalAttention(nn.Module):
"""
Implements causal attention with dropout and masking.
Args:
d_in (int): Input embedding dimension.
d_out (int): Output embedding dimension.
context_length (int): Length of the context (number of tokens).
dropout (float): Dropout rate. Default is 0.1.
qkv_bias (bool): If True, adds a learnable bias to the Q, K, V projections. Default is False.
"""
def __init__(self, d_in, d_out, context_length, dropout=0.1, qkv_bias=False):
super().__init__()
# Linear layers for K, Q, V projections
self.W_keys = nn.Linear(d_in, d_out, bias=qkv_bias)
self.W_query = nn.Linear(d_in, d_out, bias=qkv_bias)
self.W_value = nn.Linear(d_in, d_out, bias=qkv_bias)
# Dropout layer
self.dropout = nn.Dropout(dropout)
# Upper triangular mask to prevent attending to future tokens
self.register_buffer(
'mask',
torch.triu(torch.ones(context_length, context_length), diagonal=1)
)
def forward(self, x):
"""
Forward pass for causal attention.
Args:
x (torch.Tensor): Input tensor of shape (batch_size, num_tokens, d_in).
Returns:
torch.Tensor: Context vectors of shape (batch_size, num_tokens, d_out).
"""
b, num_tokens, d_in = x.shape
# Compute keys, queries, and values
keys = self.W_keys(x)
query = self.W_query(x)
values = self.W_value(x)
# Calculate attention scores
att_scores = query @ keys.transpose(1, 2) # Transpose to get (batch_size, num_tokens, num_tokens)
# Apply mask to prevent attending to future tokens
att_scores.masked_fill_(self.mask.bool()[:num_tokens, :num_tokens], -torch.inf)
# Compute attention weights
attn_weights = torch.softmax(att_scores / keys.shape[-1]**0.5, dim=-1)
# Apply dropout to attention weights
attn_weights = self.dropout(attn_weights)
# Compute context vectors
context_vec = attn_weights @ values
return context_vecThe CausalAttention class takes additional arguments context_length and dropout to specify the maximum sequence length and the dropout probability, respectively. It also registers the mask as a buffer to ensure it is properly moved to the appropriate device along with the model.
In the forward method, we apply the mask to the attention scores using masked_fill, ensuring that future tokens are ignored. We then apply the softmax function, perform dropout regularization, and compute the context vectors as before.
By using the CausalAttention class, we can easily incorporate causal attention and dropout regularization into our self-attention-based models, enabling them to handle tasks that require masking future tokens.
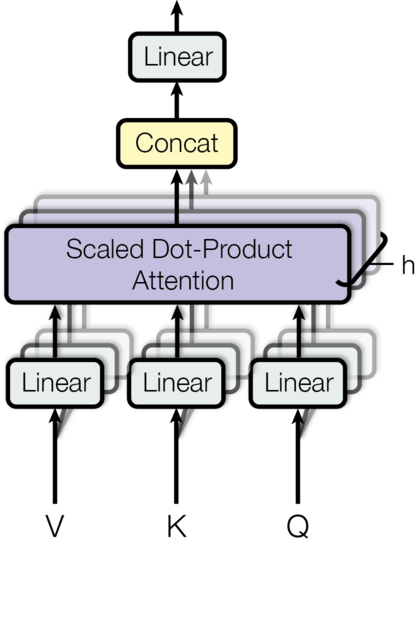
Multi-Head Attention
Multi-head attention is an extension of the self-attention mechanism that allows the model to attend to different parts of the input sequence in multiple ways simultaneously. Instead of performing a single attention operation, multi-head attention splits the input embeddings into multiple smaller matrices (heads) and applies self-attention to each head independently. The results from all heads are then concatenated and linearly transformed to produce the final output.
The motivation behind multi-head attention is to enable the model to capture different types of relationships and dependencies within the input sequence. Each head can focus on different aspects of the input, allowing the model to learn a more diverse and nuanced representation.
Here's a step-by-step breakdown of the multi-head attention process:
Splitting the Input Embeddings: The input embeddings are split into multiple smaller matrices, each representing a different head. The number of heads is a hyperparameter that can be tuned based on the specific task and model architecture. If the input embeddings have dimension
d_outand there arenum_headsheads, each head will have a dimension ofd_head = d_out // num_heads.Applying Self-Attention to Each Head: For each head, the input embeddings are projected into query, key, and value matrices using separate linear transformations. The self-attention mechanism is then applied to each head independently, computing the attention scores, attention weights, and context vectors for each head.
Concatenating the Head Outputs: The context vectors from all heads are concatenated along the embedding dimension to form a single matrix. This concatenated matrix has a dimension of
d_model, which is the same as the original input embeddings.Linear Transformation: The concatenated matrix is passed through a final linear transformation to produce the output of the multi-head attention mechanism. This linear transformation allows the model to combine and mix the information from different heads.
class MultiHeadAttention(nn.Module):
def __init__(self, d_in, d_out, num_heads, context_length, dropout):
super().__init__()
assert (d_out % num_heads == 0), "d_out must be divisible by num_heads"
self.d_in = d_in
self.num_heads = num_heads
self.head_dim = d_out // num_heads
# Linear layers for Q, K, V projections
self.W_query = nn.Linear(d_in, d_out)
self.W_key = nn.Linear(d_in, d_out)
self.W_value = nn.Linear(d_in, d_out)
# Linear layer to combine head outputs
self.out_proj = nn.Linear(d_out, d_out)
# Dropout layer
self.dropout = nn.Dropout(dropout)
# Upper triangular mask to prevent attending to future tokens
self.register_buffer(
"mask",
torch.triu(torch.ones(context_length, context_length), diagonal=1)
)
def forward(self, x):
batch_size, num_tokens, d_in = x.shape
# Compute keys, queries, and values
keys = self.W_key(x) # (batch_size, num_tokens, d_out)
queries = self.W_query(x) # (batch_size, num_tokens, d_out)
values = self.W_value(x) # (batch_size, num_tokens, d_out)
# Reshape to (batch_size, num_tokens, num_heads, head_dim)
keys = keys.view(batch_size, num_tokens, self.num_heads, self.head_dim)
queries = queries.view(batch_size, num_tokens, self.num_heads, self.head_dim)
values = values.view(batch_size, num_tokens, self.num_heads, self.head_dim)
# Transpose to (batch_size, num_heads, num_tokens, head_dim)
keys = keys.transpose(1, 2)
queries = queries.transpose(1, 2)
values = values.transpose(1, 2)
# Calculate attention scores
attn_scores = queries @ keys.transpose(2, 3)
# Shape: (batch_size, num_heads, num_tokens, num_tokens)
# Apply mask to prevent attending to future tokens
mask_bool = self.mask.bool()[:num_tokens, :num_tokens]
attn_scores.masked_fill_(mask_bool, -torch.inf)
# Compute attention weights
attn_weights = torch.softmax(attn_scores / keys.shape[-1]**0.5, dim=-1)
# Apply dropout to attention weights
attn_weights = self.dropout(attn_weights)
# Compute context vectors
context_vec = attn_weights @ values
# Shape: (batch_size, num_heads, num_tokens, head_dim)
# Reshape and combine heads
context_vec = context_vec.transpose(1, 2) # (batch_size, num_tokens, num_heads, head_dim)
context_vec = context_vec.contiguous().view(batch_size, num_tokens, -1)
# (batch_size, num_tokens, d_out)
# Apply final linear projection
context_vec = self.out_proj(context_vec) # (batch_size, num_tokens, d_out)
return context_vec
The __init__ method initializes the necessary parameters and modules for multi-head attention:
It takes the input dimension
d_in, output dimensiond_out, number of headsnum_heads, context lengthcontext_length, and dropout probabilitydropout.It asserts that
d_outis divisible bynum_headsto ensure proper splitting of dimensions.It initializes the linear transformations for the query, key, and value matrices (
self.W_query,self.W_key,self.W_value) and an additional output projection matrix (self.out_proj).It also registers the causal mask as a buffer using
self.register_buffer().
The forward method performs the multi-head attention computation:
It applies the linear transformations to the input
xto obtain the query, key, and value matrices (queries,keys,values).It splits the matrices into multiple heads by reshaping and transposing the tensors. The resulting shape is
(batch_size, num_heads, num_tokens, head_dim), wherehead_dimisd_out // num_heads.It computes the attention scores by performing matrix multiplication between the queries and keys using the
@operator. The resulting shape is(batch_size, num_heads, num_tokens, num_tokens).It applies the causal mask to the attention scores using
masked_fill_(), setting the upper triangular part to negative infinity. This ensures that each token can only attend to the tokens that appear before it in the sequence.It applies the softmax function to the masked attention scores to obtain the attention weights. The scaling factor
keys.shape[-1]**0.5is used to stabilize the gradients.It computes the context vectors by multiplying the attention weights with the values using the
@operator. The resulting shape is(batch_size, num_heads, num_tokens, head_dim).It transposes and reshapes the context vectors to
(batch_size, num_tokens, d_out)to combine the outputs from all heads.It applies the output projection matrix (
self.out_proj) to the combined context vectors to obtain the final output.
The MultiHeadAttention class efficiently implements multi-head attention by performing the computations in a single pass. It takes advantage of tensor operations and reshaping to parallelize the computations across multiple heads.
By using this efficient implementation, the model can capture different types of relationships and dependencies within the input sequence, allowing it to learn more expressive and nuanced representations for various natural language processing tasks.
The MultiHeadAttention class can be used as a building block in larger models, such as the Transformer architecture, to leverage the power of multi-head attention in a computationally efficient manner.
The GPT Architecture: Harnessing the Power of Multi-Head Attention
The GPT (Generative Pre-trained Transformer) architecture, which includes models like GPT-2 and GPT-3, has revolutionized the field of natural language processing. At the core of the GPT architecture lies the multi-head attention mechanism, which enables the model to capture rich linguistic patterns and generate coherent and contextually relevant text.
For comparison, the smallest GPT-2 model (117 million parameters) has 12 attention heads and a context vector embedding size of 768. The largest GPT-2 model (1.5 billion parameters) has 25 attention heads and a context vector embedding size of 1,600. The embedding sizes of the token inputs and context embeddings are the same in GPT models (d_in = d_out).
Here's a code snippet showcasing the initialization of the multi-head attention module in the GPT-2 architecture:
torch.manual_seed(123)
# Sample inputs for num_heads = 12, d_in = d_out = 768, context_length = 1024
batch = torch.rand(2, 1024, 768)
# Two inputs with 1024 tokens each; each token has embedding dimension 768.
print(batch.shape)
batch_size, context_length, d_in = batch.shape
d_out = 768
num_heads = 12
mha = MultiHeadAttention(d_in, d_out, num_heads, context_length, 0.0)
context_vecs = mha(batch)
print(context_vecs)
print("context_vecs.shape:", context_vecs.shape)
Conclusion
In this blog post, we have explored the concept of attention mechanisms and their significant impact on natural language processing tasks. Starting with a simplified version of self-attention and progressing to the more advanced and efficient multi-head attention, we have seen how attention allows models to selectively focus on relevant parts of the input sequence and capture long-range dependencies effectively. Self-attention enables each token to attend to every other token in the sequence, facilitating the learning of rich, context-dependent representations. Multi-head attention takes this a step further by allowing models to capture different types of relationships and dependencies simultaneously, enhancing their expressive power and ability to understand and generate natural language.
Congrats on sticking with the blog and understanding the importance of attention in coding the GPT-style models from scratch. Implementing attention mechanisms, especially multi-head attention, is crucial for building the Transformer architecture. By delving into the details and implementing it efficiently, you’ve gained valuable insights into the core component that powers many top-notch NLP models.
Thanks for reading NeuraForge: AI Unleashed!
If you enjoyed this deep dive into AI/ML concepts, please consider subscribing to our newsletter for more technical content and practical insights. Your support helps grow our community and keeps the learning going! Don't forget to share with peers who might find it valuable. 🧠✨
Connect with me on LinkedIn.



